Mở đầu
Đây là phần thứ 4 trong loạt bài viết khám phá về zk-SNARK, một công nghệ cho phép chứng minh sự đúng đắn của một kiến thức mà không cần phải tiết lộ thông tin bí mật. Ở những phần trước, chúng ta đã tìm hiểu một số khái niệm phức tạp như Quadratic Arithmetic Program và Elliptic Curve Pairings (cop link phần 3 vào chữ tô đậm này).
Quadratic Arithmetic Program cho phép biểu diễn các bài toán tính toán bằng các đa thức, và Elliptic Curve Pairings cung cấp một công cụ mã hóa hữu ích cho việc kiểm tra tính đúng đắn của dữ liệu. Bằng cách kết hợp chúng với một số thuật toán khác, chúng ta có thể cho phép người chứng minh chứng minh rằng họ biết giải pháp cho một QAP cụ thể mà không tiết lộ bất kỳ điều gì khác. Điều này mang lại sự tin cậy mà không cần tiết lộ dữ liệu nhạy cảm.
Bài viết này sẽ tập trung vào Pinocchio Protocol for QAP , cho phép chứng minh rằng một biến thỏa mãn một số điều kiện nhất định mà không cần phải tiết lộ thông tin chi tiết về giá trị của biến đó.
Chứng minh này dễ dàng tạo ra và có thể được xác thực mà không cần kiểm tra từng bước tính toán, đảm bảo tính riêng tư và bảo mật của dữ liệu trong các ứng dụng blockchain và các lĩnh vực khác đòi hỏi sự xác thực an toàn và hiệu suất cao mà không tiết lộ thông tin riêng tư.
Non-zero-knowledge Pinocchio Protocol Construction
Chúng ta bắt đầu bằng việc minh họa cách hoạt động của giao thức Pinocchio như sau:
Đặt G là 1 nhóm có thứ tự nguyên tố p. Đặt E : Fp → G là một mã hóa đồng cấu(homomorphic encoding). Cụ thể như sau:

cho một generator g
Đặt

Biểu thức trên là một “bilinear map” của đường cong Elliptic. Giả sử người chứng minh P biết một nhân chứng như bên dưới

cho mạch số học ban đầu. Bằng cách rút gọn, cô ấy sẽ biết một số đa thức sao cho

Đến đây, ta sẽ vẫn thấy hơi khó hiểu đúng không! Đừng lo lắng, hãy đọc kỹ lại từng dòng và nghiền ngẫm các công thức, tôi sẽ giải thích ý tưởng chính của giao thức này ngay bên dưới!
V(verifier) muốn kiểm tra P(Prover) tại một điểm ngẫu nhiên(random point) z ∈ Fp đối với các giá trị của đa thức trên. P được truy vấn về giá trị của


và h(z) tại một số z ∈ Fp ngẫu nhiên. P sẽ mã hóa đồng cấu(homomorphically encode) những giá trị này và gửi chúng đến V . Nhờ vào các thuộc tính homomorphic và bilinear map , V có thể xác minh rằng giá trị được mã hóa đồng cấu thỏa mãn cùng một phương trình (20) ở phía trên.
Nếu như làm vậy, Verifier có thể tin chắc rằng Prover thực sự biết một nhân chứng mà không cần tìm hiểu về nhân chứng đó. Dưới đây là thông tin chi tiết hơn về ý chính vừa được mô tả.
Bước đầu tiên của giao thức là tạo ra một Common Reference String (CRS), chứa các homomorphic encoding của các bội số của z.
CRS sẽ phục vụ cho 2 mục đích:
Thứ nhất, Prover có thể tạo ra homomorphic encodings cho chứng minh của mình bằng cách sử dụng tổ hợp tuyến tính(linear combinations) của các phần tử nhóm của CRS mà không cần biết z.
Thứ hai, việc thiết lập CRS loại bỏ nhu cầu V phải tạo z theo cách thủ công và gửi tin nhắn có mã hóa từ z đến P. Điều này cho phép bằng chứng này hoàn toàn không tương tác(non-interactive), vì sau khi CRS được tạo, P có đủ khả năng để tạo ra bằng chứng thuyết phục.
Chúng ta có thể coi CRS như hai tập hợp thành phần nhóm công khai:
The evaluation key, chứa những thành phần nhóm cần thiết để xây dựng proof và verification key, chứa các thành phần cần thiết để xác minh.
Common Reference String(Chuỗi tham chiếu chung):
Chọn ngẫu nhiên α, βu, βv, βw, γ, z ∈ F ∗ p .
Triển khai CRS dưới đây, sau đó loại bỏ tất cả các phần tử nhóm được sử dụng trong quá trình tạo ra nó (toxic waste).


Prover’s message:
Giả sử Prover có đa thức như sau:

Đầu tiên Prover sẽ tính toán h(x). Khi đó, bằng chứng của người chứng minh bao gồm những điều sau đây:
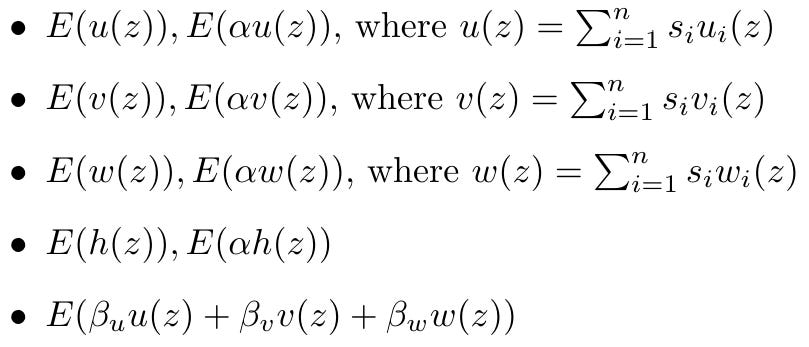
Verification:
Khi nhận được bằng chứng của người chứng minh, trước tiên người xác minh sẽ kiểm tra xem các thuật ngữ u(z), v(z), w(z), h(z) có được xây dựng dưới dạng tổ hợp tuyến tính của các thuật ngữ trong CRS hay không, thực hiện 4 lần kiểm tra sau:
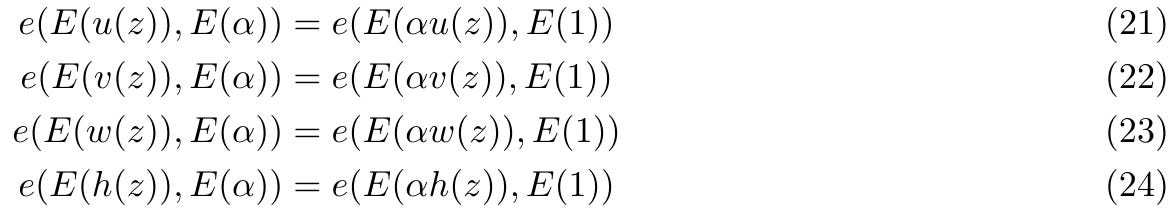
Tiếp theo, kiểm tra xem mỗi thuật ngữ u(z), v(z), w(z) có được tạo bằng cách sử dụng cùng các hệ số tuyến tính không:
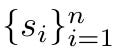
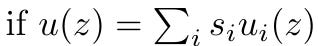
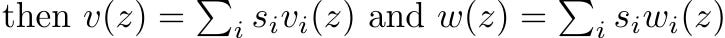
Điều này có thể được kiểm tra bằng cách xác minh phương trình sau:
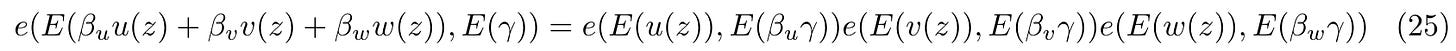
Cuối cùng, ta kiểm tra key condition đặc trưng cho tiêu chí chia hết đa thức:

Ta đã thành công xây dựng Non-zero-knowledge Pinocchio Protocol khi và chỉ khi tất cả các kiểm tra từ (21) đến (26) giữ nguyên.
Tiếp theo ta sẽ đến bước phân tích Non-zero-knowledge Pinocchio Protocol nhé!
Non-zero-knowledge Pinocchio Protocol Analysis
Trước tiên, ta cần tìm hiểu Knowledge of Exponent Assumption
Giả sử Alice được cung cấp một cặp phần tử nhóm (x, αx)
Ta gọi một cặp như vậy là α−separated. Sau đó, đối với Alice, việc tạo ra một cặp α−separated khác (y, αy) là không khả thi, ngoại trừ việc tạo ra nó theo cách sau đây:

Nếu được cung cấp n cặp α−separated , nếu Alice trả lại một cặp α−separated khác, thì nó phải là một tổ hợp tuyến tính của các cặp α−separated ban đầu với xác suất cao.
Quay trở lại giao thức của chúng ta, điều kiện chính mà V cần kiểm tra là điều kiện chia hết đa thức:

Tuy nhiên, ngoài phương trình này, cần có các phương trình khác mà người xác minh cũng phải kiểm tra.
Điều này là vì có thể cho Prover tạo ra các giá trị thỏa mãn phương trình này, nhưng không được tạo ra từ một chứng nhân thực sự s cho mạch số học. Để đảm bảo điều này, Verifier cần một cách để kiểm tra rằng các đa thức mà Prover sử dụng thực sự là một tổ hợp tuyến tính của các đa thức cơ sở trong CRS.
Giả định “Knowledge-of-Exponent” hữu ích vì nếu một cặp phần tử nhóm mà Prover gửi và một cặp đã cho đều là α− separated, cặp của Prover phải được tạo ra như một tổ hợp tuyến tính của các cặp α− separated đã cho.
Do đó, Verifier có thể sử dụng một hàm ghép để kiểm tra một cách hiệu quả rằng hai cặp này đều là α− separated, để đảm bảo Prover đã tạo ra bằng cách sử dụng một phương án thỏa mãn thực sự của mạch số học. Cụ thể hơn, đối với hai cặp (x, αx),(y, αy), điều sau đây đúng:
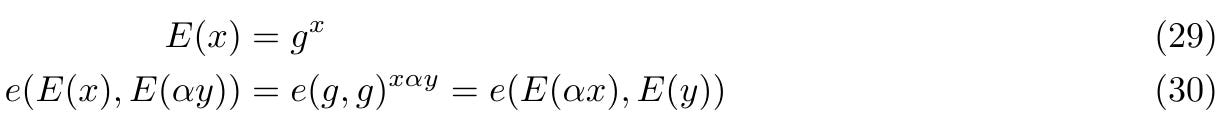
Verifier có thể sử dụng điều này để thực hiện kiểm tra sau đây:
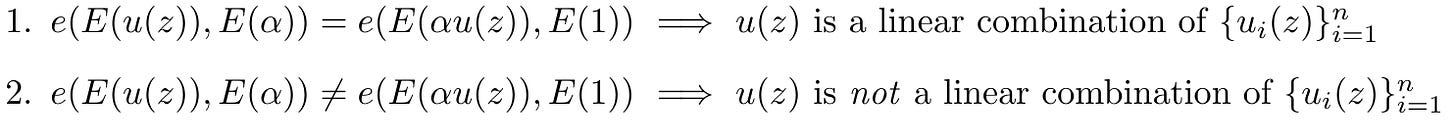
Sử dụng ý tưởng này, người xác minh cần xác minh ba điều:

Từ đó, ta có thể chứng minh được giao thức Pinocchio thỏa mãn 2 tính chất là completeness and soundness.(Đoạn chứng minh này khá phức tạp, các bạn có thể đọc thêm nguồn tài liệu mình để bên dưới để hiểu rõ hơn nhé!)
Zero-knowledge Pinocchio Protocol Modification
Về cơ bản, nếu người xác minh V tạo ra chứng minh của riêng họ s’ = (s’₁, s’₂, …, s’ₙ), họ có thể tính toán E(u'(z)), E(v'(z)), E(w'(z)), E(h'(z)) theo giao thức của người chứng minh.
Nếu các giá trị này khác biệt so với E(u(z)), E(v(z)), E(w(z)), E(h(z)), mà người chứng minh tính toán bằng s, thì người xác minh kết luận rằng bằng chứng của người chứng minh không phải là s’ (Explaining SNARKs Part VI: The Pinocchio Protocol)
Để loại bỏ vi phạm “zero-knowledge” này, người chứng minh P thêm một dịch chuyển ngẫu nhiên(random shift) vào các đa thức u, v và w (Pinocchio: Nearly Practical Verifiable Computation)
Random shift sẽ là một bội số của t(x), để mọi thứ vẫn giống nhau mod t(x). Đối với δ₁, δ₂, δ₃ ngẫu nhiên thuộc Fp, được lựa chọn ngẫu nhiên:

Sau đó, P sẽ đánh giá chúng tại z bằng CRS và gửi thuật ngữ đã dịch chuyển(shifted terms) trong bằng chứng của mình thay cho các thuật ngữ chưa dịch chuyển(unshifted terms) tương ứng.
Như vậy là đã hoàn thành xong bước Zero-knowledge Pinocchio Protocol Modification rồi, tới đây mọi người đã thấy lú não chưa=))))))
Nhưng đó là tất cả rồi, một lần nữa rất cảm ơn các bạn vì đã đọc tới đây. Nếu bạn thích bài viết này, đừng quên theo dõi và để lại một tràng pháo tay.
Vậy là kết thúc một loạt các bài viết về “Khám phá zk-SNARK” của mình, rất mong các bạn để lại những đóng góp để mình có thể hoàn thiện hơn và có động lực viết những bài tiếp theo!
Nguồn bài viết: Team Tech/Research AlphaTrue
Nguồn tham khảo:
- Chen, T., Lu, H., Kunpittaya, T., & Luo, A. (2022). A review of zk-snarks. arXiv preprint arXiv:2202.06877. https://arxiv.org/pdf/2202.06877.pdf